Digital Chaos Generator: Цифровой генератор хаоса. Немного теории.

Вначале приведу теорию по генератору фрактального сигнала.

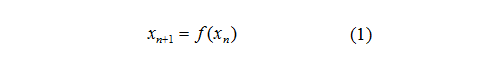
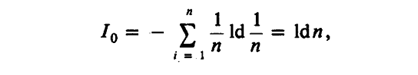
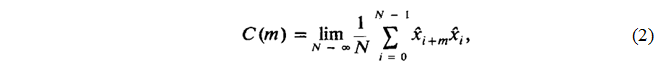
Часть 1. Введение в хаос.

В классической динамике при изучении законов Ньютона нам говорили, что если заданы силы, действующие между частицами, а также начальные положения и скорости частиц, то с помощью достаточно мощного компьютера можно предсказать движение или развитие системы (эволюцию) для любого сколь угодно позднего момента времени. Однако появление быстрых компьютеров не привело к обещанной бесконечной предсказуемости в динамике. Напротив, совсем недавно было обнаружено, что движение некоторых очень простых динамических систем не всегда можно предсказать на большой интервал времени. Такие движения были названы хаотическими, и их исследование привлекло в динамику некоторые новые математические идеи. [1. стр. 10] . В физике образцом хаотического явления остается турбулентность. А осознание того, что хаотическая динамика свойственна всем нелинейным физическим явлениям, вызвало революцию в современной физике.

        Мы должны различать так называемые случайные и хаотические движения. Первый термин относится к ситуации, когда мы действительно не знаем действующих сил или знаем только некоторые статистические характеристики параметров. Термин «хаотический»  применяется в тех детерминированных задачах, где отсутствуют случайные или непредсказуемые силы или параметры. Вот выдержка из очерка Пуанкаре «Наука и метод»: «… иногда небольшая разница в первоначальном состоянии вызывает большое различие в окончательном явлении. Небольшая погрешность в первом вызвала бы огромную ошибку в последнем. Предсказание становится невозможным…»

        В современной литературе термин  «хаотический»  применяется к таким движениям в детерминированных физических и математических системах, траектории которых обнаруживают сильную зависимость от начальных условий.

        На рис. 1 показаны примеры механических систем, динамика которых хаотична. Первый пример – мысленный эксперимент с идеализированным бильярдным шаром (здесь пренебрегается твердотельное вращение шара), который ударяется и отскакивает от сторон эллиптического бильярдного стола. Если соударения упругие, то энергия сохраняется, но для эллиптических столов определенной формы шар блуждает по столу, никогда не повторяя в точности свою траекторию.

        Другой эксперимент: шар в потенциале, состоящем из двух ям. Когда стол, на котором стоит прибор, не колеблется, такой шар имеет два состояния равновесия. Однако, если стол колеблется, совершая периодическое движение достаточно  большой амплитуды, шар начинает беспорядочно перепрыгивать из одной ямы в другую; таким образом, периодическое воздействие на одной частоте вызывает неупорядоченный отклик с широким спектром частот. Возбуждение непрерывного спектра частот, расположенного ниже частоты воздействия, является одной из примечательных особенностей хаотических колебаний рис.2.[1, стр.13]

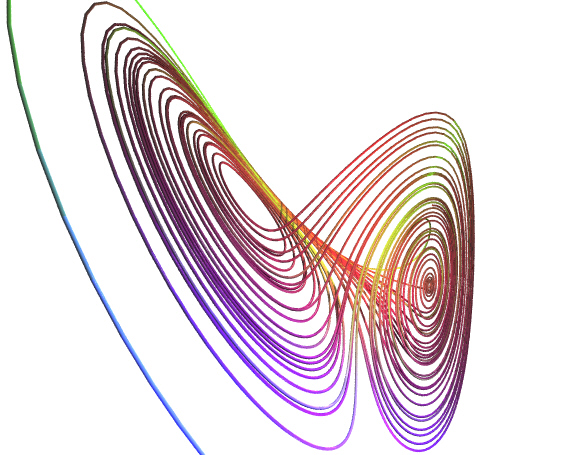
     Может возникнуть вопрос: «Если в хаотических системах невозможны предсказания, то разве в них может присутствовать какой-либо порядок?».  Для диссипативных¹ систем ответ на этот вопрос утвердителен; хаотическая динамика развивается в рамках определенной структуры. Эту структуру нелегко усмотреть с помощью обычных методов изучения динамики, например откладывая зависимость отклика от времени или получая частотный спектр. Этот порядок следует искать в фазовом пространстве (по осям которого отложены координата и скорость, т.е. координата – производная). Здесь можно обнаружить, что хаотические движения обладают новым геометрическим свойством, называемым фрактальной структурой.

        Целью является – научиться выявлять фрактальные структуры в хаотических колебаниях, а также количественно описывать потерю информации в этих движениях, так похожих на случайные.

---

[1] Термин «диссипативный» означает, что произвольно выбранный в фазовом пространстве элементарный объем V, ограниченный поверхностью S, сжимается.

Часть 2.Характеристики хаотического движения.

ПОКАЗАТЕЛЬ ЛЯПУНОВА.

     Под действием отображения

              

соседние точки могут разбегаться, что ведет к хаотическому движению. Показатель Ляпунова  λ(х0) характеризует степень экспоненциального разбегания [2]. Определение показателя Ляпунова выглядит следующим образом:

     Отсюда следует, что exp( λ(х0) ) - это коэффициент растяжения, он указывает, во сколько раз в среднем увеличится за одну итерацию расстояние между очень близкими точками.

        Кроме того, показатель Ляпунова определяет среднюю потерю информации (о положении точки в [0,1]) за одну итерацию. Разобьем интервал [0,1] на n равных подынтервалов, и предположим, что точка x0 может оказаться в каждом из них с вероятностью (1/n). Узнав какой из подынтервалов содержит x0, мы имеем информацию

где ld – логарифм по основанию 2. Если мы уменьшаем n, то информация Io уменьшается и при n=1 становится равной нулю.

        Объясним свойство потери информации с других позиций [1]. Предположим, что мы можем измерить координату с точностью Δx, а скорость – с точностью Δv. Разделим теперь плоскость координата-скорость (называемую фазовой плоскостью) на ячейки площадью ΔxΔv,показанные на рис. 3

     Если начальные условия заданы с конечной точностью, то мы знаем, что система находится где-то в заштрихованной области на фазовой плоскости рис.3, а. Но если система хаотична, то эта неопределенность со временем растет, увеличиваясь до размера N(t)  ячеек, показанных на рис.3, б. Увеличение неопределенности, описываемое законом

является вторым характерным свойством хаотических систем. Постоянная h связана с понятием энтропии в теории информации. Так же в [1] ее связывают с показателем Ляпунова.

    

КОРРЕЛЯЦИОННАЯ ФУНКЦИЯ

        Корреляционная функция для отображения (1)  определяется следующим образом:

Из этого определения следует, что C(m) представляет еще одну характеристику стохастичности итерационной последовательности x0, f(x0),f^2(x0)… . Эта характеристика показывает, насколько отклонения от среднего значения

вычисленные через m шагов (т.е. x(i+m) и x(i) ) , связаны в среднем друг с другом [2].

        Подытоживая, отметим, что последовательность итераций x0, f(x0),f^n(x0) может быть охарактеризована с помощью:

1)   показателя Ляпунова, который показывает, как разбегаются близкие точки под действием f ;

2)   корреляционной функции C(m) , которая измеряет зависимость между итерациями через m  шагов.

СТРАННЫЙ АТТРАКТОР.

Аттрактор – множество точек или подпространство в фазовом пространстве, к которому приближается траектория после затухания переходных процессов[1] (предельное множество траекторий в фазовом пространстве системы, к которому стремятся все траектории из некоторой окрестности этого множества [3]). Если это предельное множество есть устойчивое состояние равновесия – аттрактор системы будет неподвижной точкой; если это устойчивое периодическое движение – аттрактором будет замкнутая кривая, называемая предельным циклом.

Раньше считалось, что аттрактор есть образ исключительно устойчивого режима функционирования системы. Сейчас пришли к пониманию того, что режим детерминированного хаоса – тоже аттрактор в смысле определения предельного множества траекторий в ограниченной области фазового пространства. Однако такой аттрактор имеет два существенных отличия: траектория такого аттрактора непериодическая (она не замыкается) и режим функционирования неустойчив (малые отклонения от режима первоначально нарастают). Именно эти различия и привели к необходимости ввести в рассмотрение новый термин, предложенный математиком Ф.Такенсом, «странный аттрактор» [3].

        Странный аттрактор обладает следующими свойствами [2]:

• он является аттрактором, т.е. занимает ограниченную область фазового пространства, к которой по истечении большого интервала времени притягиваются все достаточно близкие траектории из так называемой области притяжения. Область притяжения может иметь очень сложную структуру. Кроме того, сам аттрактор состоит из одной траектории, т.е. траектория с течением времени должна пройти через каждую точку аттрактора;
• свойство, делающее аттрактор странным – чувствительность к начальным условиям, т.е., не смотря на сжатие в объеме, не происходит сокращения длин во всех направлениях и расстояния между первоначально сколь угодно близкими точками на аттракторе через достаточно большое время становятся конечными.

Все обнаруженные к настоящему времени странные аттракторы имеют дробную хаусдорфову размерность. Пока не ясно, всегда ли дробность хаусдорфовой размерности следует из свойств, описанных ранее, или она необходима дополнительно для странного аттрактора.

Обычно странный аттрактор возникает, когда фазовый поток сжимает элементарный объем в одних направлениях и растягивает его в других. Чтобы оставаться в ограниченной области, элементарный объем одновременно складывается. Этот процесс растяжения и складывания порождает хаотическое движение траектории на странном аттракторе.

Итак, каков же критерий «странности»? Как установлено теоретиками им является неустойчивость траектории. Причем неустойчивость обязана быть экспоненциальной! Это означает, что малое возмущение режима D(0) должно во времени увеличиваться по экспоненте:

где λ - показатель Ляпунова.

Оказалось, что положительность величины λ говорит не только об экспоненциальной неустойчивости режима колебаний, но доказывает наличие в системе перемешивания. Если установлено, что исследуемый режим имеет положительный показатель Ляпунова λ>0, то следствием будут:

·         непериодичность в зависимости от времени любой из координат состояния;

·         сплошной спектр мощности (в спектре колебаний присутствуют все частоты из некоторого интервала);

·         спадающая во времени автокорреляционная функция.

    До недавнего времени с таким поведением указанных характеристик однозначно связывали представления о случайном процессе. Теперь же полагают, что подобными свойствами может обладать процесс, порождаемый детерминированными законами. Это обстоятельство и послужило основанием называть такие процессы детерминированным хаосом.

ЛИТЕРАТУРА

1. Мун Ф. Хаотические колебания: Вводный курс для научных работников и инженеров: Пер. с англ. – М.: Мир, 1990. – 320 с.
2. Шустер Г. Детерминированный хаос: Введение: Пер. с англ. – М.: Мир, 1988. – 240 с, ил.
3. Анищенко В.С. Знакомство с нелинейной динамикой: Лекции соросовского профессора: Учеб. пособие. Москва-Ижевск: Институт компьютерных исследований, 2002. 144 с.